DEFINIÇÃO DE FILTROS DE HARMÔNICOS

João Roberto Cogo

Escola Federal de Engenharia de Itajubá

Av. BPS, 1303 – Caixa Postal 50 – 37500-000 – Itajubá – MG – Brasil

Fone: (035)622-1613 – Fax: (035)622-2337

Artigo publicado na Revista Eletricidade Moderna
Ano XXIII, nº 255 – Junho de 1995 – página 110 à 116 e página 129

RESUMO

A nova portaria do DNAEE (Departamento Nacional de Águas e Energia Elétrica) n° 1569 de 23/12/93 estabeleceu que o fator de potência de referência, a partir de março de 1994, seria de, no mínimo, 0,92.
Assim, pode-se prever que a instalação de bancos de capacitores no sistema elétrico Brasileiro deverá ser da ordem de 6 [GVAr], principalmente, ao se verificar que a partir de 01 de Abril de 1996, o fator de potência de referência será medido através de uma média hora a hora ao invés da média mensal atual. Logo, os problemas devido ao impacto da instalação destas unidades capacitivas nos sistemas elétricos industriais se caracterizam por ressonâncias, sobre tensões e sobrecargas e, para evitá-las, os filtros de harmônicos aparecem como candidatos naturais nos locais onde cargas elétricas especiais se fazem presentes.
Assim, o objetivo deste trabalho é de apresentar os critérios para a definição dos filtros de harmônicos, para a correção do fator de potência, no sentido de evitar ressonâncias em freqüências múltiplas da fundamental desenvolvendo-se, para tal finalidade, expressões específicas.

1   – INTRODUÇÃO

Para a caracterização do problema relativo às cargas elétricas especiais junto a bancos de capacitores considera-se o sistema elétrico apresentado na FIGURA 1 a seguir.

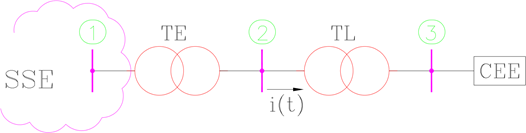
FIGURA 1 – SISTEMA EM ANÁLISE.

Na FIGURA 1 tem-se:

SSE – Sistema de suprimento de energia (da concessionária ou da própria indústria); TE – Transformador de entrada do sistema que contem a carga elétrica especial; TL – Transformador do alimentador da carga elétrica especial; CEE – Carga Elétrica Especial; i(t) – Corrente no primário de TL.

O diagrama unifilar de impedâncias para a análise do efeito dos harmônicos de corrente provenientes das cargas elétricas especiais para o sistema da FIGURA 1 está mostrado na FIGURA 2 com banco de capacitores e com filtros instalados na barra 2. Admite-se que o sistema de suprimento de energia foi substituído por uma reatância indutiva conectada entre a referência e a barra 1. A carga elétrica especial foi substituída por uma fonte de corrente. Caso na barra 2 não existam bancos de capacitores ou mesmo filtros de harmônicos, a tensão RMS em módulo devido aos harmônicos de corrente pode ser obtida a partir da FIGURA 2.a, da seguinte forma:

U2n = n . XS1 . In

Note que:

XS₁ = ^XEQ₁ + ^XTE₁                e          ^Xsn = ^XEQn + ^XTEn = n . ^XS₁

Fazendo-se I_n igual a 1[pu], na base de cada harmônico tem-se:

U₂n = n . ^XS1

ou seja, o valor da impedância é equivalente a tensão na base do harmônico de corrente.

2   – EFEITO DA INSTALAÇÃO DOS BANCOS DE CAPACITORES

Caso seja colocado na barra 2 um banco de capacitores para a correção do fator de potência, tem-se como diagrama de impedâncias para o harmônico de ordem n aquele mostrado na FIGURA 2.b. Da FIGURA 2.b pode-se escrever:

U&2n = ( ^jX_jXSn_Sn) (₋−_jX^jX_CnCn₎) .I&n = Z&2n n.I&

Calculando-se a tensão e ainda considerando-se In igual a 1[pu] na base de cada harmônico tem-se (em módulo):

U₂n = ^Z₂n       (2) onde:

Z&2n = j.⎜ XCn − XSn ⎟⎠= j .⎝⎜ XC1 − n12 . X1S1⎟⎠   ⎝   Na expressão anterior considerou-se:	(3)
X XSn = n . XS1 e XCn =           C1	(4)

                      ⎛ XSn . XCn ⎞            ⎛ n X.     S . XC ⎞

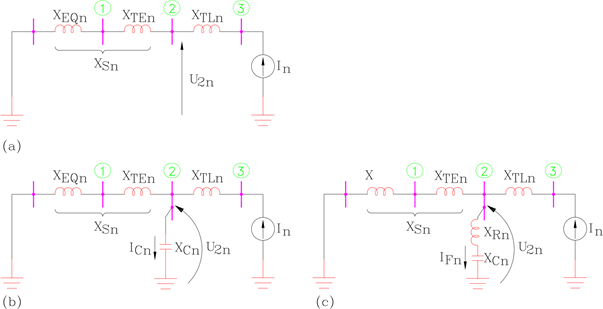
FIGURA 2 – DIAGRAMA DE IMPEDÂNCIA PARA O HARMÔNICO DE CORRENTE DE ORDEM N. a – SEM BANCO DE CAPACITORES E REATORES NA BARRA 2; b – COM BANCO DE CAPACITORES NA BARRA 2; c – COM FILTROS DE HARMÔNICOS NA BARRA 2.

Por outro lado, o valor da reatância capacitiva na freqüência fundamental, para a condição de ressonância, poderá ser relacionado com a reatância indutiva do sistema através de:

XC1 = nS2 . XS1   Levando-se a expressão (5) na (3) tem-se:	(5)
Z&2n = jXS1 .⎢ .nS2 ⎤⎥ ⎡ n	(6)

⎣nS2 − n2 ⎦

O valor da corrente no ramal do banco de  capacitores  (tomando por

base que I_n = 1 [pu] para cada harmônico, FIGURA 2.b), é dado por:

n2

Icn = 2 n_S2₎                                                                                                                (7)

₍n ₋

De acordo com a expressão (5), caso o valor de n_S seja 5 (n_S = 5)

significa que a potência do banco de capacitores é 25 vezes inferior a potência de curto na barra onde o mesmo será instalado e, se existir um harmônico de corrente de quinta ordem (n = 5) haverá uma ressonância, ou seja, o valor da corrente (vide equação (7)) será infinito.

Ou por outro lado, caso o banco de capacitores entre em ressonância com o sistema para o harmônico de ordem n = n_S implica, neste caso, que a tensão na barra 2 poderá ser infinita (vide equações (2) e (6)).  A corrente que passa pelo banco de capacitores está ilustrada na FIGURA 3 para diversos valores de ns.

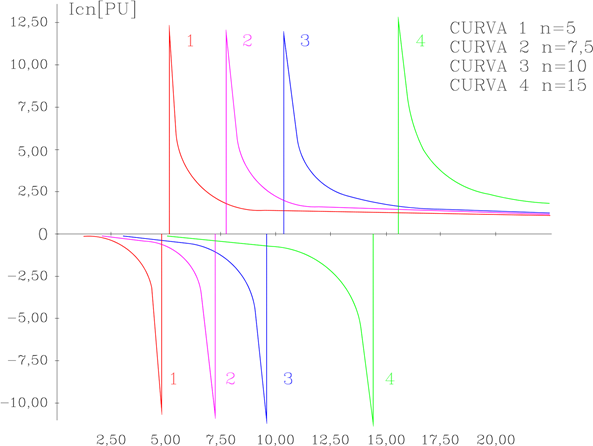
FIGURA 3 – CURVA CARACTERÍSTICA DE CORRENTE NO CAPACITOR EM FUNÇÃO DA ORDEM DO HARMÔNICO EXISTENTE TOMADO COMO SENDO DE 1 [PU].

3   – INSTALAÇÃO DE FILTROS

Caso no lugar do banco de capacitores se instale filtros sintonizados tem-se, para o harmônico de ordem n, o diagrama de impedâncias mostrado na FIGURA 2.c, onde a impedância equivalente (de THEVENIN) a partir da barra 2, é dada por:

Z&2Fn = ((jXjXSnSn).(−−jXjXCnCn++jXjXRnRn))                                                                        (8)

Para o sistema da FIGURA 2.c, fazendo-se a ressonância do filtro

ocorrer para uma freqüência n₀ vezes a fundamental, tem-se:

XC1

=n X0 . _R1 (9) n0

Com base nas expressões (5) e (9) pode-se escrever:

⎛nS ⎞2

X_R1 =⎜          ⎟ . ^X_S1                                                                                                                       (10)

⎝n0 ⎠

Com base em (5) e (10) a expressão (8) torna-se:

                                 ⎧⎪        n nn

Z^&₂Fn = jXS1 .⎨⎪[(        [(2 S )nn2 S−)(2n nS o− (n n) ]S o2 ) ]2 ⎬⎪⎭⎫⎪     (11) ⎩ nno) + (

A expressão (11) assume o valor infinito para n = NR dado por:

n n^{S . 0}

NR=                                                                                                                                           (12)

n₀2 +n_S2

Analogamente ao item anterior, o valor da corrente I_fn (vide FIGURA 2.c) é dado por:

(nno)2

IFn = ( 2 nnS )2 − (n nS o)2    (13) nno) + (

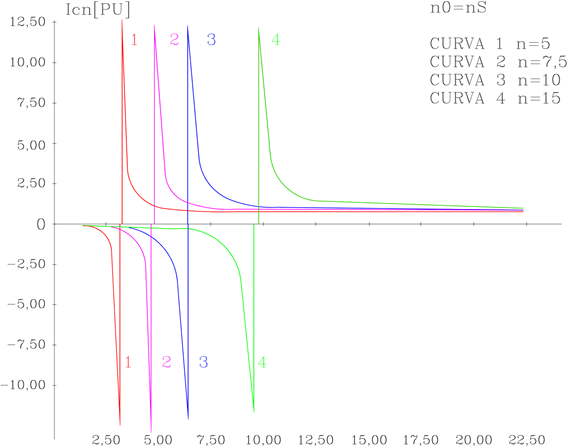
A curva característica para os mesmos valores de n_S definidos na FIGURA 3 do item anterior é apresentada na FIGURA 4.

4   – DEFINIÇÃO DO FILTRO DE HARMÔNICO

Para a definição da tensão nominal do banco de capacitores (U_BCN) após a inclusão do reator em série (FIGURA 2.c) recomenda-se de modo a garantir a sua vida útil que atenda a expressão a seguir:

U_BCN                               ^XC . I    ^XCn . ^In            (14) n=2

e a potência reativa nominal (Q_BCN) do banco de capacitores deve ser no mínimo de :

QBCN                                 ^XC I²           ( . ^XCn . ^In²)    (15) n=2

Como o valor de X_C1 nas expressões (14) e (15) depende exatamente de

Q_BCN e U_BCN que pretende-se determinar, adota-se, inicialmente, que:

UBCN =ξ.^U₁                                                                                                                              (16)

onde U1 é o componente da tensão na freqüência fundamental do sistema elétrico, onde o filtro será instalado. Note que, praticamente, o valor de ξ deve ficar compreendido entre:

1,06 ≤ ξ ≤ 1,35                                                                                                                         (17)

Visto que a correção do fator de potência é feita na freqüência

fundamental em função da potência ativa e do fator de potência atuais (conta de energia elétrica mensal) pode-se, inicialmente, estimar que a potência reativa na freqüência fundamental para corrigir o fator de potência é dada por:

Q₁ ≅ P{tg [arc(cos(FP_A))]− tg [arc(cos(FP_D))]}                                                                   (18)

Na expressão (18) tem-se:

P – potência ativa média;

FP_A – fator de potência atual;

FP_D – fator de potência desejado (recomenda-se adotar 0,94).

Assim, para uma primeira estimativa, visando eliminar as inequações

(14) e (15), adota-se:

QBCN = Q1 .ξ2   Logo com base nas equações (16) e (19) tem-se:	(19)
U 2 XC1 = 1	(20)

Q₁

Assim, a partir deste valor inicial de X_C1 retorna-se às equações (14) e (15) para se calcular os valores reais de U_BCN e Q_BCN do banco de capacitores e a reatância X_R1 do reator a ser adquirido.

Recomenda-se, portanto, a seguinte seqüência:

1. – Defina Q₁ usando-se a equação (18)
2. – Calcule X_C1 usando-se a equação (20)
3. – defina X_R1 como sendo

XC1 fR

XR1 =        2 .

no

 1,03≤ fR ≤1,05 ou 0,93 ≤ fR 0,97

Adote inicialmente que n_o = n_s sendo n_s definido conforme equação (5).  OBS: Nunca deve-se adotar: 0,97 ≤ ^f_R ≤ 1,03

1. – Calcule U_BCN de acordo com o lado direito da inequação (14). 5 – Calcule Q_BCN de acordo com o lado direito da inequação (15). 6 – Calcule o novo ξ

UBCN

ξ=              

U₁

• – Calcule Q_BCN de acordo com a equação (19).
• – Compare o resultado do passo 7 com o resultado do passo 5 se maior pare; se menor faça:

^{XC1 =} [U_Q^BCNBC_N((passopasso47)])2

• – Retorne ao passo 3.

Para a visualização dos pontos de ressonância considere a TABELA 1, a

seguir, a qual ilustra os valores obtidos considerando-se:

1 – A variação da freqüência da carga elétrica especial de 0,01 em 0,01 vezes a freqüência fundamental. Em outras palavras, fez-se uma varredura em freqüência, dada por:

F = ∆n . F_rede

onde ∆n assumiu uma faixa de valores desde zero até 1,5.n variando de 0,01 em 0,01 sendo que, nas diversas simulações, adotou-se:

n = 3, 4, 5, 6, 7, e 11

valores estes típicos para as cargas elétricas especiais.

5   – CONCLUSÕES

Conforme nota-se na TABELA 1 a instalação de um filtro para um

determinado harmônico muda o valor da freqüência de ressonância relativamente àquela que se teria caso fosse colocado na rede apenas um banco de capacitores.

Por exemplo, a instalação apenas de capacitores na rede com

possibilidade de ressonância para o quinto harmônico (n_S = 5,001) levaria a se ter uma elevação na tensão da rede de:

• 12754 vezes a impedância do sistema (X_S1) para cada unidade de corrente produzida pela carga elétrica especial.

porém, ao instalar um filtro no lugar deste banco para o quinto harmônico (n_O = 5,00) tem-se que o valor da tensão agora passa a ser zero neste harmônico. Todavia, para o harmônico correspondente a ordem 3,54 (NC = 3,54) vezes a freqüência fundamental. A elevação de tensão seria:

• 759 vezes a impedância do sistema para cada unidade de corrente produzida pela carga especial nesta freqüência, sendo infinita para a ordem 3,536 (NR = 3,536).

Assim, percebe-se que a freqüência de sintonia onde ocorrerá

ressonância fica alterada sempre para um valor correspondente à freqüência menor que aquela original de ressonância.

Como os valores de freqüência que não são múltiplos inteiros da

fundamental (acima de uma vez a fundamental) é difícil de ser encontrado, deve-se precaver ao construir um filtro, de modo que não se tenha a ocorrência de valores para NC e NR em um número próximo a valores inteiros principalmente caso a Carga Elétrica Especial o tenha como harmônico característico. Cabe-se ressaltar que os valores obtidos para Z_2n foram para uma varredura na freqüência de 0,01 em 0,01. Caso se faça a varredura com valores diferentes destes, novos resultados são obtidos os quais podem ser maiores ou menores. Todavia, a medida que a varredura leve a se ter NC = NR, os valores serão bastante elevados. Na prática, deve-se projetar o filtro escolhendo-se valores de X_R1 e X_C1

de modo que NR não seja inteiro ou fique próximo de um número inteiro. Na falta de uma melhor informação do sistema, fazendo-se X_R1 = 6% de X_C1 tem-se obtido bons resultados na prática.

	TABELA 1 – VALORES OBTIDOS PARA Z2n e Z2Fn
nS	Z2n	nO	Z2Fn	NC	NR
3,001	4491,864	2,91 3,00 3,09	1191,076 672,305 425,800	2,090 2,120 2,150	2,089 2,122 2,153
4,001	7976,949	3,88 4,00 4,12	405,074 1642,064 7449,159	2,790 2,830 2,870	2,785 2,829 2,870
5,001	12754,040	4,85 5,00 5,15	1803,654 759,064 1479,937	3,480 3,540 3,590	3,482 3,536 3,588
6,001	18803,940	5,82 6,00 6,18	1997,747 1505,593 999,538	4,180 4,240 4,310	4,178 4,243 4,305
7,001	26220,140	6,79 7,00 7,21	1397,237 74197,260 2408,771	4,870 4,950 5,020	4,874 4,950 5,023
11,001	71692,600	10,67 11,00 11,33	15697,940 9724,307 6302,435	7,660 7,780 7,890	7,659 7,779 7,893

Na TABELA 1 tem-se:

• n_S; Z_2n; n_O; Z_2Fn e NR: já definidas anteriormente;
• NC: é o valor de n que fornece para cada par (n_S, n_O) o máximo valor de Z_2Fn considerando uma variação incremental em n de 0,01 em 0,01.

6  – NOMENCLATURA UTILIZADA

U₁ – Componente fundamental da tensão na barra 2;

U_2n – harmônico de tensão de ordem n na barra 2;

X_S1 – reatância equivalente vista da barra 2 na freqüência fundamental; n – ordem do harmônico existente (n = 2, 3, 4, 5, …);

I_n – harmônico de corrente de ordem n obtido através da decomposição em série trigonométrica de FOURIER para o sinal de corrente i(t) apresentado na FIGURA 1;

X_EQn=nX_EQ1 – Reatância do sistema calculada para o n-ésimo harmônico; X_TEn=nX_TE1 – Reatância do transformador calculada para o n-ésimo harmônico;

X_Cn=X_C1/n – Reatância do banco de capacitores calculada para o n-ésimo harmônico;

X_EQ1 – Reatância do sistema calculada para a freqüência fundamental;

X_TE1 – Reatância do transformador de entrada calculada para a freqüência fundamental;

X_C1 – Reatância do banco de capacitores calculada para a freqüência fundamental;

X_R1 – Reatância do reator do filtro de harmônicos calculada para a freqüência fundamental;

S_CC – Potência de curto-circuito equivalente na barra 1;

X_S1 – Reatância equivalente ‘vista da barra 2’ na freqüência fundamental;

Z_2n – Impedância equivalente “vista da barra 2” para o harmônico de ordem n.

Note que em [Ω], o valor de X_EQ1 pode, aproximadamente, ser calculado

como:

XEQ1 = (Ubarra 1)2/SCC

7   – REFERÊNCIAS BIBLIOGRÁFICAS

• – Cogo, J.R. Critérios para Dimensionamento de Filtros de Harmônicos. X Congreso Chileno de Ingeniería Eléctrica – Universidad Austral de Chile – Valdívia, Chile – 22/11/93 – 25/11/93.
• – Cogo, J.R. Analysis of the Reactive Power Consumption and the Harmonics Injected in the Network by the Non-Linear Electrical Loads. IV Symposium of Specialists in Electrical Operational and Expansion Planning, 23-27-Maio-1994, Foz do Iguaçú, Brasil.