João Roberto Cogo, Hector Arango, Jocélio Souza de Sá

Escola Federal de Engenharia de Itajubá – EFEI

Caixa Postal: 50  Telex: 031-3485

CEP: 37.500 – Itajubá – MG – Brasil

Artigo apresentado no IV Congresso Chileno de Ingeniería Eléctrica – Pontifícia Universidade Católica de Chile

Santiago – Chile – 11 a 15 de novembro de 1985 – pgs. 308 a 314

RESUMO

Este trabalho tem por objetivo apresentar o procedimento realizado para calcular o fluxo harmônico em um sistema industrial, através de um programa digital.
Além de apresentar o modelo usado no programa digital para o cálculo do fluxo harmônico, este trabalho tem como principal finalidade realizar uma comparação entre os resultados obtidos em cálculos com aqueles conseguidos através de medições realizadas com analisador de espectro harmônico, em um sistema industrial caracterizado por uma fábrica de papel.

1 – INTRODUÇÃO

O presente trabalho surgiu com o intuito de determinar as causas que propiciaram a explosão de um banco de capacitores de 900 [KVAr], 25 [KV] do sistema elétrico industrial de uma fábrica de papel (CIP).
Após a explosão do banco de capacitores, instalado no sistema elétrico, fez-se a substituição do mesmo por outro de maior potência 1200 [KVAr], porém de mesma tensão. Desta forma, visando prever problemas futuros neste banco, iniciou-se um trabalho de simulações e medições.
Assim sendo, apresenta este trabalho toda metodologia empregada, bem como os resultados de medições e simulações mais importantes.

2 – CONSIDERAÇÕES GERAIS

A utilização de pontes conversoras para se obter corrente contínua, provoca injeção de harmônicos, por vezes indesejáveis no sistema AC de suprimento de energia.
A FIGURA 1 ilustra uma ponte conversora, em formação de GRAETZ, de 6 pulsos. Na FIGURA 2 temse a corrente em um das fases que alimenta este conversor, sem considerar o efeito da impedância do sistema de suprimento de energia (sem “OVERLAP”) e considerando-se o efeito da impedância do sistema de suprimento de energia (com “OVERLAP”).

A forma de onda apresentada na FIGURA 2, embora alternada, não é senoidal. Desta maneira a produção de harmônicos de corrente é inevitável (os componentes harmônicos da corrente podem ser obtidos da decomposição em série trigonométrica de FOURIER). As ordens dos harmônicos obedecem a seguinte lei de formação:

n = 6q ± 1 ……………………………………………………………. (1) onde:

Os harmônicos que obedecem a equação (1) são chamados harmônicos característicos, pois aparecem com a ponte operando em condições ideais.

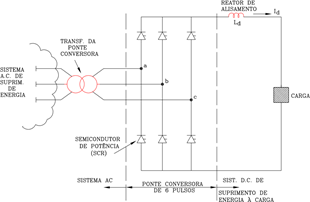
FIGURA 1 – Ponte conversora controlada de 6 pulsos.

FIGURA 2 – Corrente em uma das fases que alimenta uma ponte conversora de 6 pulsos

O valor eficaz de um componente harmônico de ordem n qualquer obedece, sem “OVERLAP”, a seguinte expressão:

0,78

I_n =          I_d n onde:

I_n – valor de corrente eficaz do componente harmônico de enésima ordem. n – ordem do harmônico I_d – valor médio da corrente no lado D.C.

Considerando-se o efeito de “OVERLAP” e um sistema perfeitamente equilibrado de suprimento de energia pode-se verificar que o valor do harmônico de corrente de ordem n (I_n) varia com a impedância do sistema A.C. de suprimento e com valor do ângulo de disparo da ponte conversora.

Todavia na prática, além dos harmônicos, citados anteriormente, harmônicos com outras ordens podem ser gerados pelas pontes conversoras. Estes componentes harmônicos são os chamados “harmônicos não característicos”. Estes não obedecem a lei de formação dada em (1).

As               principais              causas   do           aparecimento       dos harmônicos não característicos são:

2.1 – Erro intrínseco dos sistemas de disparo dos tiristores das pontes conversoras.

2.2 – Desequilíbrio das tensões dos sistemas A.C. de suprimento de energia das pontes conversoras.

2.3 – Desequilíbrio das impedâncias, por fase, dos transformadores e/ou do sistema A.C. de suprimento de energia das pontes conversoras. 2.4 – Situações anormais de operação do sistema A.C. tais como falta de uma fase ou curto-circuito.

3 – MODELO DOS COMPONENTES QUE COMPÕEM O SISTEMA EM ESTUDO

O sistema em estudo é composto basicamente de:

• linha de transmissão e cabos
• transformadores
• bancos de capacitores
• cargas

-concessionária

O modelo usado para cada um destes componentes no estudo de fluxo harmônico é apresentado a seguir.

3.1 – LINHAS DE TRANSMISSÃO E CABOS À

FREQÜÊNCIA INDUSTRIAL

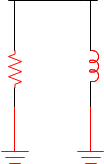
Para as linhas de transmissão e cabos utilizou-se o circuito π com a reatância capacitiva concentrada nas extremidades como mostra a FIGURA 3.

FIGURA 3 – Modelo de linha e de cabos.

• – TRANSFORMADORES         À            FREQÜÊNCIA

INDUSTRIAL

No caso dos transformadores, considerou-se apenas a resistência ôhmica dos enrolamentos e a reatância de dispersão como ilustra a FIGURA 4.

FIGURA 4 – Modelo do transformador.

3.3 – BANCO DE CAPACITORES E REATORES À FREQÜÊNCIA INDUSTRIAL

Os bancos de capacitores e reatores Shunt são representados como ilustra a FIGURA 5.a e 5.b, os reatores série como ilustra a FIGURA 5.c.

FIGURA 5 – Representação de capacitores e reatores.

a – capacitor shunt b – reator shunt

c – reator série

3.4 – CARGAS

No sistema em análise as cargas são bem caracterizadas nas barras, e sendo constituídas por:

• pontes conversoras
• motores de indução trifásicos
• caldeira elétrica

Neste estudo, considerou-se que as pontes conversoras são as únicas fontes de harmônicos de corrente e, portanto são representadas como fonte de correntes nas barras em que as mesmas se encontram.

Já os motores de indução, pelo fato de serem em número bastante elevado nas diversas barras que compõem o sistema, foram representados por elementos Shunt R, L. Como ilustra a FIGURA 6.a.

A caldeira elétrica como é uma carga com característica resistiva bem definida foi representada como ilustra a FIGURA 6.b.

^Rcarga

^Rcaldeira

a)                      b)

FIGURA 6 – Representação das cargas a – motores de um modo geral b – caldeira

3.5 – CONCESSIONÁRIA

O sistema de suprimento de energia é feito em alta tensão (138 [KV]) e neste caso a concessionária foi representada simplesmente por uma reatância indutiva Shunt caracterizada pela sua potência de curto-circuito (como ilustra a FIGURA 5.b).

4 – OBTENÇÃO DOS DADOS PARA SIMULAÇÃO DO FLUXO HARMÔNICO

Neste ponto deve-se destacar que os dados necessários ao estudo de fluxo harmônico aparecem em todas as freqüências, desde a fundamental até praticamente a 63ª.
Todavia, a experiência no sistema em pauta, através de medições prévias ao estudo, mostra que a partir do 23º harmônico os valores de distorção de tensão no barramento são bastante pequenos. Desta forma, toda simulação e feita até o 23º harmônico.
Com os dados do sistema devido a equipamento de medição (tensão , corrente e potência) serem à freqüência industrial os dados foram obtidos, quando medidos, nesta freqüência, vide item 4.1 e para os harmônicos foram obtidos como ilustra o item 4.2.

4.1 – LEVANTAMENTO DOS DADOS DO SISTEMA ELÉTRICO À FREQÜÊNCIA INDUSTRIAL

4.1.1 – Cabos

Os cabos utilizados neste trabalho são Eprotenax, aterrado, 25 [KV], fabricante Pirelli. Os comprimentos estão dados na FIGURA 7. As características construtivas foram obtidas diretamente do fabricante. Desta forma os dados para R, X_L e X_C que compõem o circuito π foram obtidos diretamente do fabricante.
Toda linha aérea considerada como sendo constituída de cabo 2 [AWG] de cobre nú, e com a configuração da linha obtida no campo, utilizou-se o programa EMTP (versão EFEI) para obter-se os valores de R, X_L e X_C.
Para potência de curto-circuito da concessionária, obteve-se o valor junto a mesma que no caso é de 3021,148 [MVA] e considerando se este valor como sendo totalmente reativo.

4.1.2 – Representação das cargas que não sejam pontes conversoras

As cargas que constituem o sistema elétrico da CIP, exceto as pontes conversoras, são caracterizadas pela representação RL paralela (conforme recomendação de referências internacionais [1], [2], [3] e [4]). Através de cálculos e principalmente de medições determinou-se as potências ativas (P) e aparente (S).
As medições de potência, tensão e corrente foram feitas no lado primário dos transformadores (T₃, até T₂₀) à freqüência industrial com e sem pontes conversoras. Assim sendo, subtraindo-se as perdas ativas e reativas dos transformadores pode-se calcular a potência ativa (P) e aparente (S) que representam as cargas que não sejam as pontes conversoras. Estas cargas são basicamente, motores de indução de potência normalmente menor que 150 [Hp]. Apenas no transformador T₉ existe uma caldeira elétrica onde o valor de potência ativa dissipada pela mesma é bastante conhecido, mas também neste ponto fez-se as medições.
Assim sendo, tem-se:

P

FP =       ……………………………………………………………….(2)

S logo, conforme [3], para modelo de carga usado tem-se:

−               1

R_L =      (valor em por unidade, [pu]) ………………(3)

S.FP

−                        1

X _L =S(1−(FP)₂ ) (valor em por unidade, [pu]) …(4)

Com os valores de R_L e X _L as cargas passam a serem representadas em seus barramentos conforme FIGURA 6.a, através de elementos R, L ligados entre as barras de carga e terra, e a caldeira, conforme 6.b.

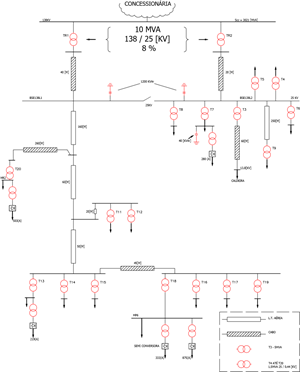
FIGURA 7 – Diagrama simplificado do sistema em análise.

4.1.3 – Representação das pontes conversoras

As pontes conversoras foram representadas conforme FIGURA 8, através de injeção de corrente.

FIGURA 8 – Representação das pontes conversoras no estudo de fluxo harmônico.
As características das pontes foram obtidas segundo levantamento de dados, no campo e catálogo dos fabricantes. Considerou-se que as pontes conversoras operavam com carga nominal, conforme características constantes em dados de fabricantes e com ângulo de disparo nominal. Além disso, as pontes conversoras em um mesmo barramento com características semelhantes, foram reunidas em uma única ponte equivalente com corrente nominal, correspondente a soma das correntes nominais das diversas pontes conversoras ali instaladas.

4.1.4 – Transformadores

Como os transformadores principais são de grande porte, os dados dos mesmos foram obtidos diretamente junto as sua placas e informações adicionais dos fabricantes e os valores das resistências e reatâncias indutivas foram convertidas em [pu] à base do sistema de modo convencional.

4.2 – LEVANTAMENTO DOS DADOS À FREQUÊNCIA DE CADA HARMÔNICO

Para os harmônicos de ordem n, o sistema elétrico foi representado simplesmente, como tendo uma característica linear, mesmo as máquinas rotativas de indução que compõem o sistema elétrico. Desta forma os componentes do sistema elétrico são dados em [pu] por:

R_n = R ……………………………………………………………. (5)

−                 −X _L n = X _L .n …………………………………………………… (6)

X⁻ _cn = ^Xc ………………………………………………………… (7) n

 onde:

−

R_n – resistência para a freqüência de ordem n.

−

X _L n = reatância indutiva para a freqüência de ordem n.

−X _cn = reatância capacitiva para a freqüência de ordem n. 5 –

PROGRAMA PARA O CÁLCULO DO FLUXO HARMÔNICO UTILIZADO NA SIMULAÇÃO DIGITAL

O programa utilizado admite que as pontes conversoras são fontes de correntes que injetam os harmônicos de correntes nas barras onde elas estão instaladas.

Admite-se que as correntes tem a forma indicada na FIGURA 1 com efeito de comutação (com “Overlap”). O ângulo de comutação é calculado com base na potência de curto-circuito da barra onde a ponte conversora está instalada. A corrente I_d é a nominal da ponte, bem como o ângulo de disparo α.

No caso da ponte semiconversora da barra MP6, considerou-se o ângulo de disparo para o bloco de corrente da parte negativa como sendo nulo.

Desta forma a expansão em série trigonométrica de FOURIER, através de programa digital, fornece os harmônicos de corrente de ordem n que serão injetados no sistema.

Dado um sistema com NB barras, pode-se escrever para cada harmônico de ordem n.

⏐V _BUS ⏐_n = ⏐^Y _BUS ⏐_n^-1 . ⏐I _BUS ⏐_n ………………………..(8)

onde:

⏐V _BUS ⏐_n = Vetor das tensões harmônicas de ordem n nos barramentos do sistema.

⏐Y BUS ⏐_n = Matriz de admitância nodal do sistema para

N-ésima ordem harmônica.

⏐I _BUS ⏐_n = Vetor das correntes harmônicas de ordem n injetadas          no           sistema pelas      pontes conversoras.

A FIGURA 9 ilustra o fluxograma do programa utilizado.

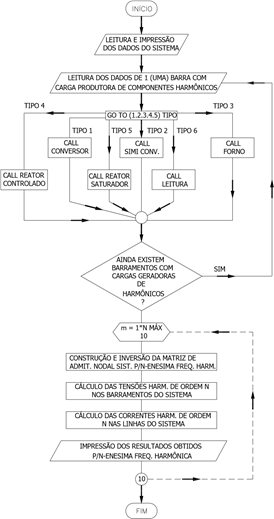
FIGURA 9 – Fluxograma do programa que calcula o fluxo harmônico.

6 – RESULTADO ESPERADO

A freqüência de ressonância esperada para o sistema elétrico em pauta nas barras BSE138L1 e BSE138L2 (vide FIGURA 7) considerando-se apenas os bancos de capacitores, pode ser calculada levando-se em conta somente o equivalente da concessionária e o transformador de 10 [MVA], como apresentado a seguir na FIGURA 10.

Para cálculo da reatância equivalente da concessionária, considerou-se os valores fornecidos pela mesma.

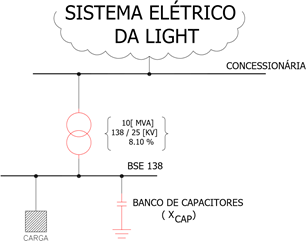
FIGURA 10 – Sistema elétrico equivalente das barras BSE138L1 ou BSE138L2.

Considerando-se a FIGURA 10, pode-se esperar que o problema de sobre tensão ocorra para o harmônico de ordem n dada por:

S^CC

n = 

S_BC onde: n – ordem do harmônico que pode provocar ressonância

S_{CC –} potência de curto-circuito na barra BSE138L1 ou BSE138L2 (FIGURA 7)

X_CONC

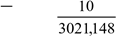
reatância                                                                    equivalente

da concessionária)

X_t ≅                                         8,1/100 = 0,081 (reatância            equivalente           do transformador)

10

S_CC =       = 118,6099 [MVA] (na barra onde

XCONC + Xt

o banco de capacitores de 120 [KVAr] está instalado).

Logo:

118,6240

n = = 9,9419

1,2

Desta forma conclui-se que é esperada ressonância harmônica para os harmônicos de ordem:

n = 7, 8, 10, 11 ou 13 com o banco de 1200 [KVAr] instalado.

O motivo de fornecer vários valores e não um valor explícito, é que os cálculos realizados neste item são aproximados e as pontes semiconversoras no caso de simulação digital de fluxo harmônico no sistema, geramos harmônicos característicos que obedecem a lei de formação: n = 3K ± 1(K=1, 2, 3…).

7 – MEDIÇÕES DOS HARMÔNICOS DE TENSÃO E CORRENTE REALIZADAS NO SISTEMA ELÉTRICO

Para realizar as medições foram utilizados os seguintes equipamentos: – Analisador de espectro harmônico Tipo 555 AM

• Impressora Tipo 555 PR
• Transformador de corrente auxiliar Classe 0,5%

Fabricante: Bonar Instrument

Procedência: Inglaterra

A TABELA 1 ilustra a distorção de tensão obtida da simulação digital nas barras BSE138L1, BSE138L2 e MR2.

A FIGURA 11 ilustra o diagrama de bloco do analisador.

Todas as medições foram realizadas na subestação conversora de 138/25 [KV] da CIP.

Os pontos onde as medições foram realizadas estão numerados de 1 a 3 e suas localizações encontram-se na FIGURA 12.

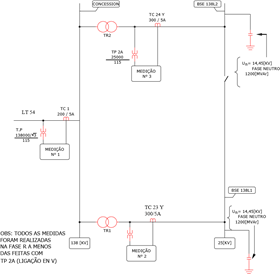
FIGURA 12 – Pontos de medição com a linha LT54.

Os sinais de corrente para o analisador vieram dos secundários dos transformadores de corrente ilustrados na FIGURA 12. E os sinais de tensão vieram dos transformadores de potencial (de núcleo magnético).

Na TABELA 2, tem-se parte dos resultados obtidos durante a medição executada nas instalações do sistema elétrico.

Os resultados apresentados pela saída do analisador de espectro harmônico encontra-se na TABELA 2 (em parte) e possuem a seguinte forma geral:

04{ {I 1F22.372 Y{ 05{ 1P23163 1H2.2833

A           B             C              D       E              F                    G

1. – ciclo de leitura
2. – tipo de harmônico amostrado: V para tensão

I para corrente 

• – valor eficaz da fundamental: tensão de Volt corrente em Ampére 
• – indica o tempo de amostragem de 10[seg]
• – ordem de harmônico amostrado
• – ângulo de fase em grau
• – valor do harmônico: – em porcentagem para tensão

– em Ampére para corrente 00 – H:M Y – horário da medição.

8 – CONCLUSÕES

O problema da ressonância provocada por harmônicos de corrente é função da configuração do sistema, e para a configuração onde fez-se as simulações e medições nota-se uma distorção de tensão bastante elevada para o harmônico de ordem 11.

Todo estudo realizado tomou-se por base o sistema elétrico, cuja configuração é dada na FIGURA 7. E com conclusão principal verifica-se que a distorção de tensão na barra BSE138L1 obtida em simulação digital é bastante elevada o que sugeriu-se a colocação de filtros (estes já foram projetados).

Nota-se ainda uma aproximação bastante grande entre os resultados medidos e os calculados em simulação digital o que comprova a validade do modelo usado, 1,7529 em simulação (TABELA 1) contra 1,79 de média dos resultados obtidos em medição (TABELA 3)

9 – REFERÊNCIAS BIBLIOGRÁFICAS

TABELA 1 – Resultado dos harmônicos de tensão e distorção harmônica (DT) obtidos nas barras BSE138L1, BSE138L2 e MR2.
OREDEM DA HARM.	TENSÕES HARMONICAS (%) – CASO 2
BSE138L1	MR2	BSE138L2
2	,0488	,0490	,0018
4	,0997	,0997	,0040
5	,7161	2,8822	,1924
7	,4035	2,5489	,2172
8	,2237	,2213	,0125
10	,2732	,2678	,0186
11	1,7529	1,6437	,2643
13	1,4292	1,1817	,1980
14	,1041	,0998	,0043
16	,0519	,0490	,0014
17	,4533	1,7323	,1151
19	,2158	1,9461	,0990
20	,0183	,0167	,0003
22	,0148	,0133	,0002
23	,2352	1,8791	,0746
DT	2,4999	5,4191	,4716

• – Harmonics in power systems – power systems Engineering series 1981 – UMIST Manchester England – September 1981.
• – Shipp, David D. IEEE Transactions on industry applications; Vol. IA-15, nº5, September/October 1979 – Harmonic analysis and supression for electrical systems supply ing static power converters and other nonlinear loads.
• – Pileggi, D.J.; Harish Chandra N.; Emanuel A.E. IEEE Transactions on power apparatus and systems, Vol. PAS-100 nº 3, March/1981 – Prediction of harmonic voltages in distribution systems.
• – Stratford, Ray P. IEEE Transactions on industry applications, Vol. IA-17, nº 1, January/February 1981. Analysis and control of harmonic current in systems with static power converters.

10 – CURRICULUM VITAE

Joao Roberto Cogo: Engenheiro eletricista pela Escola Federal de Engenharia de Itajubá em 1974; Mestre em ciências pela Universidade Federal de Santa Catarina em 1977; Professor da EFEI; Professor titular do Instituto Nacional de Telecomunicações – INATEL.

Jocélio Souza de Sá: Engenheiro eletricista pela             Escola Federal de Engenharia de Itajubá em 1969;

TABELA 2 – Parte dos resultados obtidos por medição na barra BSE138L1 (ponto de medição nº 2 da FIGURA 12).
00 12:40 Y	00 12:41 Y
15VF113.Y11P118H1.74 15IF3.52Y11P132H.050	20VF112.Y11P074H1.42 20IF3.57Y11P130H.068
00 12:40 Y	00 12:42 Y
16VF113.Y11P082H1.42 16IF3.59Y11P136H.082	21VF112.Y11P076H1.93 21IF3.56Y11P136H.067
00 12:40 Y	00 12:42 Y
17VF113.Y11P060H1.30 17IF3.59Y11P154H.071	22VF114.Y11P084H1.56 22IF3.49Y11P154H.056
00 12:41 Y	00 12:42 Y
18VF113.Y11P084H2.11 18IF3.54Y11P164H.063	23VF114.Y11P088H1.34 23IF3.57Y11P146H.058
00 12:41 Y	00 12:43 Y
19VF112.Y11P072H1.51 19IF3.58Y11P132H.074	24VF114.Y11P094H1.80 24IF3.54Y11P152H.061

Professor da EFEI.

Hector Arango: Engenheiro eletricista pela universidade Nacional del Sur (Bahia Blanca, Argentina) em 1958; Professor da EFEI.

TABELA 3 – Valores encontrados por medição, para o 11º harmônico de tensão bem como o valor médio dos mesmos.
1,46	2,11	2,12
1,99	2,51	1,67
1,26	1,42	1,80
2,29	1,93	2,25
0,98	1,56	2,37
1,80	1,34	2,40

1,89	1,80	1,65
1,74	1,78	1,58
1,42	1,87	1,73
1,30	1,96	1,85
. / .	. / .	1,79 – Média